Avanzando con IBP: De S&OP a Estrategia Integrada
En el mundo empresarial actual, donde la competencia es feroz y la agilidad es clave, la gestión eficiente de la cadena de suministro y la
Menú
Menú
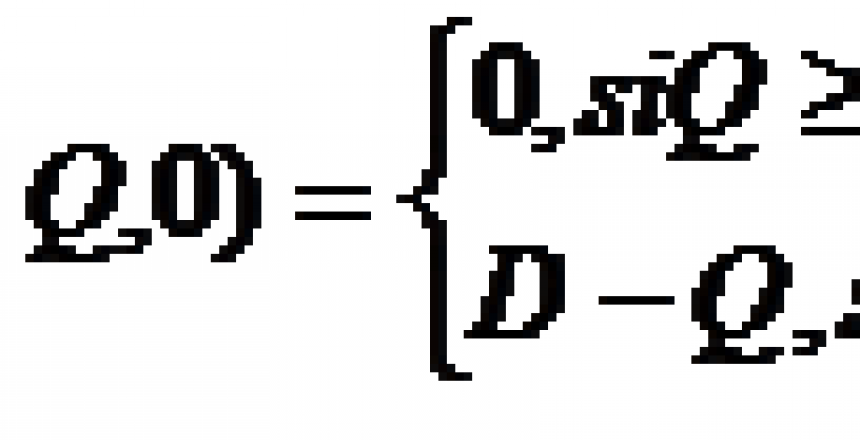
Fórmulas y métodos para ubicar las cantidades necesarias en temporada
Manejar momentos especiales de oferta requiere un cálculo detallado de las cantidades a ordenar para que la empresa tenga disponible la mercancía en el tiempo preciso y – en consecuencia – para que los clientes puedan adquirir los productos que requieren. En este artículo se presenta un modelo que facilitará el manejo de estos eventos especiales que – de no ser planificados eficientemente – podrían dejar excesos o faltantes para las organizaciones.
La gestión de inventarios requiere responder a las preguntas: ¿Qué cantidades tener? y ¿Cuándo tenerlas? La primera pregunta se refiere a un problema de cantidades y la segunda a un tema de tiempos.
Los pedidos de una sola vez se relacionan con la segunda pregunta. La cuestión es ordenar una cantidad adecuada del artículo antes del periodo en el que se requiere; este periodo puede ser una temporada, una promoción, un día, una semana, mes o año, en resumen es una situación en la que los productos se ordenen por una sola vez para cubrir una temporada.
Es por esto que a este esquema se le conoce como el “problema del vendedor de periódicos o del árbol de navidad”. Debe tenerse en cuenta que como el pedido se hace una sola vez para cubrir una temporada o un evento promocional, si este no es suficiente se presenta una escasez y en el caso contrario se presenta un exceso y habrá un sobrante.
El caso de interés se presenta cuando la demanda es aleatoria o desconocida pero que puede ser representada a través de una variable aleatoria. Todas las empresas – comerciales o de manufactura – poseen esta clase de productos, bien sea porque el comportamiento de su demanda es estacional o porque influencian la demanda a través de un evento promocional que se producirá una sola vez. En este último caso la empresa puede estar interesada – por ejemplo – en definir las cantidades que se demandarán en una campaña promocional en su principal canal de distribución.
En el caso del “distribuidor de periódicos” debe ordenar una cantidad de diarios tal que pueda atender la demanda diaria y que no le queden sobrantes; en este último escenario tendrá una penalidad por cada periódico que devuelva a la casa editorial y en el primer caso perderá la utilidad que le genera la venta de cada diario.
Cada que un producto se ordene para una temporada específica y que la demanda sea continua se puede aplicar un modelo de pedido de única vez como el que se estudiará a continuación.
Método 1: Cantidad a ordenar con demanda probabilística.
Esta sección ha sido construida tomando como referencia a Sipper y Bulfin (1998, p.p. 273-280) y a Silver et al (1998, p.p.385-410).
Considere:
D = la demanda durante el periodo de tiempo que está representada por una variable aleatoria con función de densidad de probabilidad continua f(D).
f(D) = función de probabilidad acumulada de la variable D.
Ce = el costo en que se incurre cuando hay una escasez. Es la utilidad dejada de percibir.
A = el costo de los excesos, cuando estos se presentan se deben almacenar y posteriormente realizar promociones para evacuarlos; en general se obtiene algún costo de recuperación por el exceso.
Si se tiene establecido que la demanda de un producto para una temporada puede estar dentro de un rango de ventas de {Q ,D} – donde Q es la cantidad a ordenar y D es la demanda – la cantidad máxima a vender será:
Min {Q , D}.
Una escasez estará representada por:
D – Q si D>Q(1)
Pero si no se vende lo necesario, el sobrante será:
Q – D si D<Q. (2)
Las cuatro situaciones posibles para el pedido único serán:
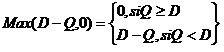(3)
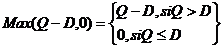(4)
Si A es el costo de almacenamiento o de exceso por unidad y Ce es el costo de faltante por unidad, para un pedido único el costo total CT es:
(5)
Y el costo esperado E(CT) será:
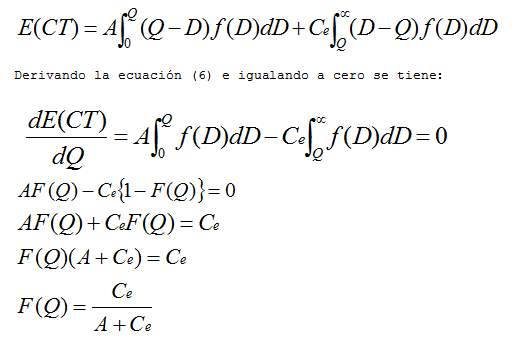(6) y (7)
Una ecuación empírica puede derivarse del caso en el que el costo de escasez es igual al costo del sobrante; esta es una situación lógica en donde el responsable de reabastecer calcula que la cantidad Q a ordenar le garantiza que la demanda total tenga el 50% de posibilidades de ser menor a Q y el 50% de ser mayor a Q.
La variable que nos ocupa es la cantidad a ordenar Q que se convierte en variable de decisión.
Sea F(D) la probabilidad acumulada de que la demanda sea menor a D, entonces el costo del exceso es AF(Q) y el costo de faltantes es [1-F(Q)]Ce . Sería necesario adquirir una cantidad Q tal que la expectativa de costos de los excesos sea exactamente igual a la expectativa de los costos ahorrados por faltantes. Para esta condición Q debería satisfacer:
(8) y Despejando F(Q) (9)
Nótese como en la ecuación (9) cuando A = Ce, entonces F(Q)= 0,5.
La solución de la ecuación (9) está representada gráficamente en la Figura No.1.
Figura No.1
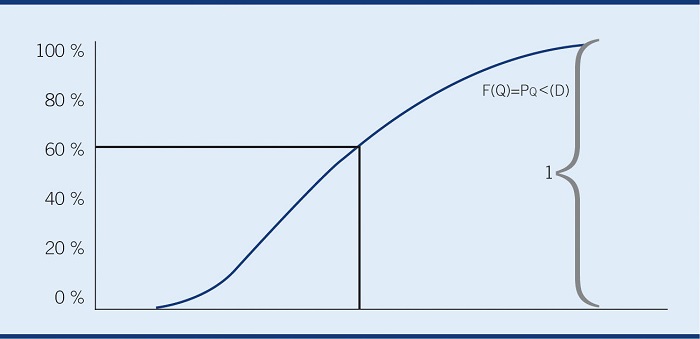
Sipper y Bulfin (1998, p. 276) han definido la razón de la ecuación (9) como razón de crítica y es un número entre 0 y 1. Esta razón crítica es la probabilidad de satisfacer la demanda durante el periodo, después de ordenar una cantidad Q para dicho periodo.
Para calcular Q – que es la variable de decisión – se debe usar la distribución de probabilidad acumulada de la distribución de probabilidades.
La razón crítica puede ser aplicada a casi cualquier situación práctica. Cuando la demanda está normalmente distribuida con media y la desviación estándar es posible obtener el valor de Q.
Una variable aleatoria normal x se estandariza restándole su media y dividiendo este resultado por la desviación estándar, de esta manera una variable aleatoria normal con = 0 y recibe el nombre de Variable Aleatoria Normal estándar y se denota como k. Lo anterior se evidencia en la Figura No.2.
Figura No.2
Campana de Gauss
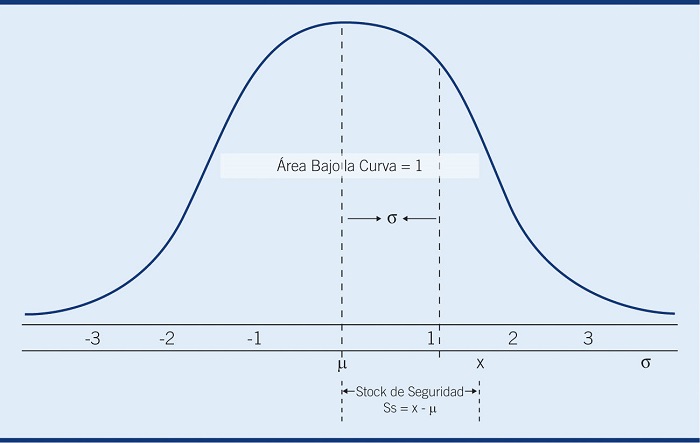
Si se llama k el número de desviaciones estándar que hay desde x a la media de la distribución se puede encontrar el valor de k con relación a la media y la desviación estándar como sigue:
Según Ross (2008 pág. 276) el valor de la variable estandarizada indica cuánto difiere la variable original de su media en unidades de desviación estándar y plantea que si – por ejemplo – la variable estandarizada k toma el valor de 2, esto significa que:
Don Abel es el dueño de una cacharrería a la cual le ha dedicado toda su vida. En la temporada decembrina él mismo se ocupaba de los pedidos de juguetes y su estrategia ha sido tener un producto destacado, innovador y de mucho impacto que haga tener flujo de compradores a la tienda.
La tienda es de unas dimensiones de 18 metros de largo y 12 de ancho y para esta temporada construye en la mitad del almacén un corral donde exhibe los juguetes, causando un gran impacto visual. Don Abel entiende que no se puede equivocar en el pedido de este juguete estelar, por eso ha recogido pacientemente la información del número de juguetes vendidos en las temporadas pasadas (ver Tabla No.1).
Tabla No.1
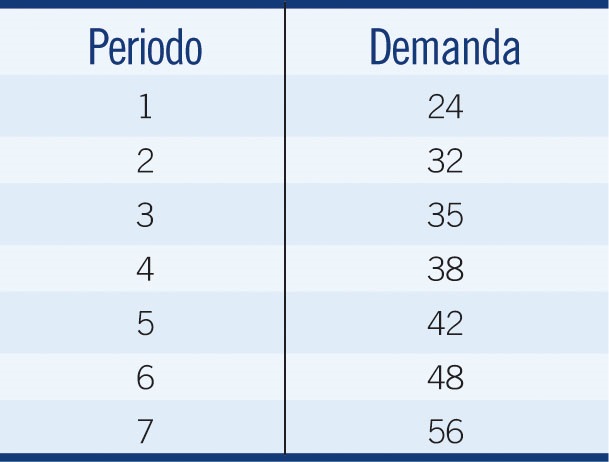
Datos Históricos de Juguetes Vendidos (Ejercicio 1)
De la tabla anterior se desprende que las ventas nunca han sido menores a 24 juguetes ni mayores a 56; se considera que cualquier demanda en este rango tiene igual probabilidad de ocurrir, por lo que la demanda es uniforme.
Si a don Abel le sobran juguetes después del 24 de diciembre, debe rebajarlos un 60% de su valor para poder deshacerse de ellos, esto no es conveniente por dos razones: la primera porque le supone una pérdida por el descuento que debe dar y la segunda porque le genera una mala imagen (los clientes no entenderán que compraron un producto a un precio elevado y 15 días más tarde lo encontrarán con una rebaja significativa). El dueño de la cacharrería analizada teme que su clientela se entere que si se espera a fin de año puede conseguir el juguete a un precio extremadamente menor.
El precio al que don Abel puede vender el juguete es $54 y la ganancia estimada por juguete es de $18. Si a este empresario se le acaban los juguetes antes del 22 de diciembre incurre en una pérdida de venta que le supone un costo igual a la utilidad que no percibe por los juguetes que hubiera podido vender si contara con las existencias adecuadas.
Don Abel ya sabe cuál será el juguete estelar de esta temporada pero debe enviar hoy mismo el pedido con las cantidades a su proveedor.
Debido a que la distribución de la demanda es probabilística se aplicará el método 1 socializado en este artículo. El método 2 no se puede aplicar debido a que la demanda no sigue un comportamiento normal.
Como la demanda puede tomar cualquier valor entre 24 y 56, la distribución es uniforme y la función de densidad es f(D)=1/(b-a):
El factor de criticidad es:
El número de juguetes que deben ordenarse se puede obtener resolviendo la probabilidad acumulada de la demanda. Resolver la ecuación es encontrar el valor Q para el cual F(Q)=0,55.
Como ya se conoce f(D) se puede despejar Q de la siguiente manera:
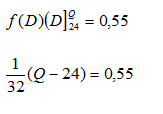
Y despejando Q se tiene:
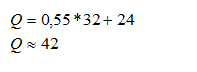
Don Abel debe pedir 42 juguetes para esta temporada. El número esperado de juguetes que faltarán es:
Por otro lado el número esperado de juguetes que quedarán en existencias es:
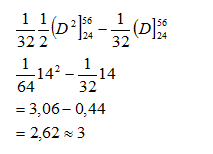
El costo total esperado de esta política será:
Nótese que no está calculado el costo de compra de los juguetes de $1.512 (42*36).
Y la utilidad esperada será:
En la economía campesina las parcelas se dedican a algún cultivo de frutas y hortalizas. Considere el caso de Manuel, quien destinó una hectárea de su pequeña finca para el cultivo de plátano artón. Él sabe que puede cortar el producto desde las 11 semanas de cultivado y hasta las 15 semanas; además su mercado natural es el mercado municipal de su pueblo natal, a donde acuden los campesinos los fines de semana a hacer sus aprovisionamientos de víveres y otras necesidades.
Manuel sabe también que puede vender en promedio 42 racimos semanales con una desviación estándar de 10. En todo caso la venta dependerá del volumen de plátano que los demás cultivadores cosechen esa semana y de la cantidad de campesinos que visitan el pueblo.
Este agricultor puede vender cada racimo de plátano en $9.000 y su utilidad estimada es de $3.500 por racimo. Cualquier racimo que no pueda vender lo debe entregar a los mayoristas que visitan el pueblo el domingo ya de tarde a un precio de $3.500, estos los lleva al mercado de la ciudad más cercana. Casi nunca le sobran racimos que el mayorista no le compre, de ser así debería donarlos al acilo del pueblo o a la iglesia para ser repartido a los pobres.
Debido a que la demanda tiene un comportamiento normal se puede aplicar el segundo método propuesto en este artículo, sin embargo vale la pena mencionar que también se puede aplicar el segundo método.
De la tabla de la distribución normal el Q óptimo se encuentra en 63,64% del área de la curva. Para ese valor k equivale a 0,35. Tenga en cuenta que de la ecuación (11) se puede calcular el número de racimos a cortar:
Paso 3: Despejar Q, de la ecuación 11.
Montgomery, Douglas C. y Runger, George C.. Probabilidad y Estadística. Aplicaciones a la Ingeniería. McGraw-Hill. México (1996).
Rodríguez Urbina, Lucía, Maya Moya, Luz Marina y Aranda Silva, Moisés. Probabilidad. 1ª Edición. Editorial Pontificia Universidad Javeriana. Bogotá (2010).
Sipper, Daniel y Bulfin Jr., Robert L. Planeación y Control de la Producción. Mc Graw Hill. México (1998).
Ross, Sheldon M. Introducción a la Estadística. Versión Española Traducida por Prof. Dr. Teófilo Valdés Sánchez. Reverté. Barcelona (2008).
Silver, Edward A., Pyke, David F y Paterson, Rein. Inventory Management and Production Planning and Scheduling. 3ra. Edición. John Wiley & Sons, Inc. Nueva York (1998).
Este es el caso de la distribución uniforme continua. Una variable aleatoria X se dice que es uniforme en el intervalo (a, b) si su función de densidad es constante dentro de él. La distribución uniforme representa la distribución de datos con la incertidumbre más completa; la función de densidad de probabilidad
Para más detalles sobre esta distribución de probabilidad continua ver Montgomery (1996 p.p.170-172) y Rodriguez et al (p.p.143-145).
Para una situación en donde la distribución de probabilidad de la demanda es discreta consulte Silver et al (1998, p.p.391-392).
{/accesstext}
En el mundo empresarial actual, donde la competencia es feroz y la agilidad es clave, la gestión eficiente de la cadena de suministro y la
Usamos el famoso proceso de S&OP (Sales & Operation Planning) como la herramienta que nos permitiría conectarnos para vencer la triple restricción y de esta
Debido a la alta demanda del mercado en rutas marítimas para el comercio internacional, la Autoridad del Canal de Panamá (ACP) aseguró que se aumentarán
El Grupo EPM presentó una planta piloto de producción de hidrógeno verde (H2V) a través de energía limpia. Este proyecto es desarrollado en conjunto por
